
The World Lighthouse Hub
N02: Latitude and Longitude

Fig. N02.1: The Earth from Space
Accurate navigation ultimately depends upon knowledge of where you are on the surface of the Earth which, for simplicity we think of as spherical. (The Earth is approximately a sphere of radius 6371 Km, or 3959 miles. There is some asymmetry but we can ignore this here.) The globe is divided into sections in two ways known as latitude and longitude. To understand this a bit better you need to become an astronaut...
Longitude
Imagine you are looking at the Earth from a point in space directly over the north pole (Figure 1). The planet looks like a circle with the pole at its centre and the equator at its circumference. Longitude is obtained by thinking of the Earth as a circle divided into 360 degrees, with 0 degrees at 12 o'clock, and clockwise going in the westerly direction. The lines of longitude radiate outwards from the centre (pole) towards the circumference. All lines of longitude meet at the poles. In fact, what you have done is to draw a series of imaginary circles around the surface of the planet so that they all meet at the poles (Figure 2). To create a standard reference point or zero, it was internationally agreed a long time ago that a line of zero degrees longitude would be defined to pass through the Greenwich astronomical observatory in London, UK.
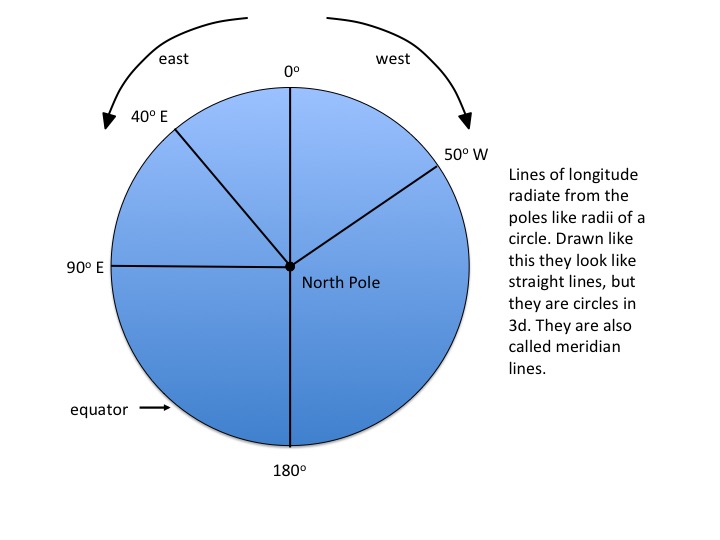
Figure N02.2: Longitude - 1
Because of the three dimensions of the Earth, the separation of lines of longitude varies depending upon your proximity to the pole. Imagine that you are now back on Earth and standing exactly at the South Pole. Take one step to the left. No matter which way you choose to do this you are walking north! So, it doesn't matter at all in which direction you face when you are standing at the south pole, you are always facing north. Now walk around the pole in a small circle. you could accomplish this in a few seconds and walk a mere one or two metres in doing so. You would have walked through all 360 degrees of longitude.
Now imagine that you are standing exactly on the equator and facing east. If you walk to the left you are going north. If you walk to the right, you are going south. If you try to walk through all 360 degrees of longitude you will walk a distance of 2 x pi x 6371 = 40,035 km! The equator is the line that divides longitude to its greatest extent.
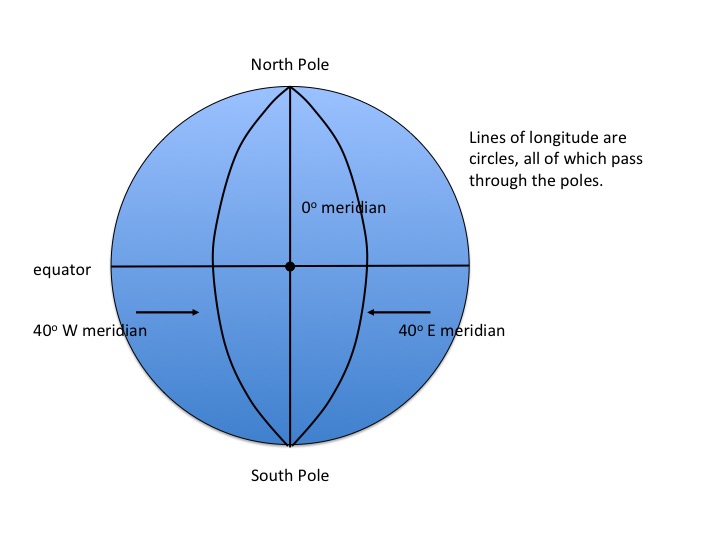
Figure N02.3: Longitude - 2
Latitude
So what about latitude? Well, take another trip in your space rocket and imagine now that you are looking at the Earth with the equator straight ahead of you and crossing the circle of the planet horizontally like a diameter; the north pole is on the top and the south pole on the bottom (Figure 3). The north pole is a point 90 degrees north of the equator, and the south pole is a point 90 degrees south of the equator. Image that you draw a line from the centre of the Earth to the surface, so that the angle from the equator (we say the angle subtended) is 40 degrees. All points on the surface of the Earth that would fall on this line are at a latitude 40 degrees. If you now turned the planet so that the pole was at the centre of the circle once more, and the equator was at the circumference, the line of latitude would look like another circle with smaller radius (Figure 4). Thus, longitude is a series of imaginary parallel circles drawn with the poles at the centre and using the equator as the circumference. Note too that there is a latitude of 40 degrees north and also one of 40 degrees south. The diagram in Figure 3 shows the 40 degree north line and one at 20 degrees south.
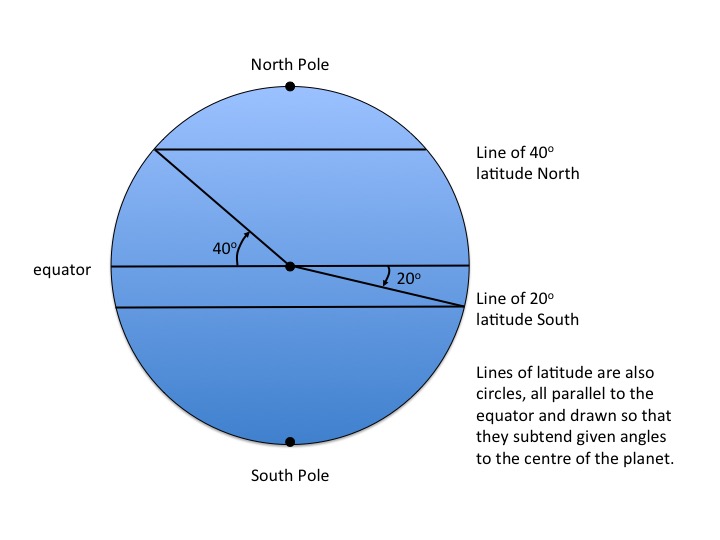
Figure N02.4: Latitude - 1
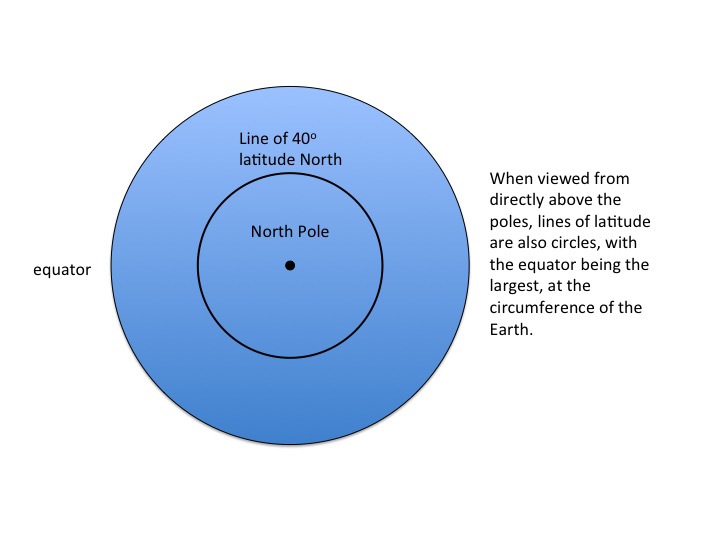
Figure N02.5: Latitude - 2
EXAMPLE OF CALCULATION WITH LATITUDE AND LONGITUDE
We can calculate the distance between two points using their latitude and longitude co-ordinates. However, there are some approximations involved, and we do need to take account of the latitude at which the calculations are made. For example, elsewhere in these pages, we have studied how Smeaton observed his own lighthouse on the Eddystone Rocks by looking at it from Plymouth Hoe. How can we calculate the distance between these two points?
First we need the latitude/longitude co-ordinates for Eddystone: 50o 10.84'N; 4o 15.94'W and for Plymouth Hoe: 50o 21.81'N; 4o 8.39'W.
Now we need to express them as decimals, bearing in mind that there are 60 minutes in 1 degree. Thus the co-ordinates become x1 = 50.180, y1 = 4.266 and x2 = 50.3635, y2 = 4.140.
The distance between the two latitudes is easy to calculate, because we simple take the Earth's circumference and divide by 360 to get the distance equivalent to 1 degree of latitude. This distance is 111.2 Km per degree. For longitude, we need to make a correction for the smaller circumference of the Earth at 50 degrees North. This is done by multiplying the circumference at the equator (40032 Km) by the cosine of 50o, to which we find that the circumference is 25729 Km. Thus at this latitude, 1 degree of longitude is equivalent to 25729/360 = 71.47 Km.
Knowing x1, x2, y1 and y2 in degrees, we can convert to distances in Km, i.e. x2-x1 = 20.33 Km; y2-y1 = 9.0 Km.
Now, all that is necessary is to use Pythagoras to calculate the hypotenuse with these two distances as the sides of the right-angled triangle. Thus the distance from the Eddystone to the How, d, is SQRT [ (x2-x1)2 + (y2-y1)2 ] giving us the answer of 22.2 Km or 13.8 miles.
In this calculation we have assumed that (1) the Earth is perfectly spherical (2) there is no significant curvature of the Earth for the distances involved and (3) that the conversion to distance at longitude 50 degrees is linear over the distance involved. All of these assumptions are justified, but they might not be if the distances were much larger.