
The World Lighthouse Hub
H06: Photometric Definitions and Calculations

Figure H06.1: Smeaton's Tower, Plymouth, UK, photographed in 2012.
Today, Smeaton's Tower stands majestically on Plymouth, where it was rebuilt in 1884 after its replacement by a larger structure on the Eddystone Rocks. The site of the Smeaton Tower today is probably where John Smeaton himself stood proudly in the late 1700s to observe his own creation. The Eddystone Rocks, indicated in the picture, are located about 14 miles from this position. The present lighthouse, built by Sir James Douglass, stands there today, and it can be seen from Plymouth Hoe only in clear weather. On the day when this photograph was taken, the weather was good and the lighthouse could be clearly seen with the naked eye, although, even in the master photograph, the 50 metre tall tower is hard to discern. Smeaton kept a diary of everything that occurred when he built his own lighthouse on the rocks. The lighthouse was lit with just 24 candles, and he wrote about the visibility of it at night. In this section, we are going to consider some of the ideas of night visibility of lights more closely.
Let's begin with the question:
Q: How can we do calculations about light observations?
To properly understand this question, we must be clear about the precise terms and ideas we are using and it is important to appreciate the physical laws and units of measurement. Below is a summary of these important terms and units.
There is also a quantitative discussion about the use of candles as aids to navigation.
ANGLE OF INCIDENCE / ANGLE OF REFLECTION
When a ray of light travelling in medium 1 (air, say), meets another medium 2 (glass, as in a mirror) and is reflected away from it, we define the angle of incidence as the angle between the light ray in medium 1 and and the normal (perpendicular) to the surface or boundary of medium 2 (Figure H06.2). The angle of reflection is the angle between the light ray in medium 1 and and the normal (perpendicular) to the surface or boundary of medium 2 after it has been reflected off the surface of medium 2. Careful measurement shows that the two angles are equal.
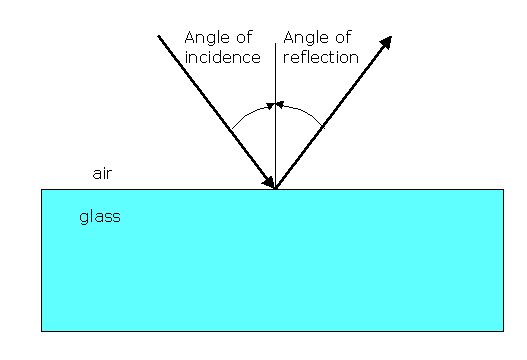
Figure H06.2: A light ray in air meets a reflective surface with an angle of incidence (shown), and is reflected away from the surface with an angle of reflection (shown) that is equal to the angle of incidence.
LUMINOUS INTENSITY

Figure H06.2: A candle can be thought of as (approximately) a point light source with a luminous intensity of 1 candela that emanates uniformly in all directions around it.
It was natural to use the candle as a baseline for light intensity in the early days of physics. For many years, light was measured in candle-power (cp). There was even a unit called the international candle, and because of the relationship with distance, people talked about brightness in foot-candles. We should try to forget these ideas today.
As science progressed, the unit of luminous intensity was redefined as the candela (cd) and it is now a base unit in the standard European system of measurements known as SI (Systeme Internationale). The conversion between them is 1 cd = 0.982 cp, so they are approximately equal, but not precisely so.
A common candle emits light with a luminous intensity of roughly one candela. If emission in some directions is blocked by an opaque barrier, the emission would still be approximately one candela in the directions that are not obscured.
By definition, the candela is the luminous intensity, in a given direction, of a source that emits monochromatic radiation of frequency 540×1012 hertz and that has a radiant intensity in that direction of 1 / 683 watt per steradian, i.e. 0.001464 W sr-1.
ELECTROMAGNETIC RADIATION AND LIGHT
Remember that we are constantly surrounded by electromagnetic radiation across a huge spectrum of wavelengths, from radio waves, microwaves, infra-red (heat), visible, ultra-violet and X-rays. (Gamma rays are present only in nuclear radiation, which is not normall present in our environment.) These days our mobile phones and other wi-fi devices work on a great deal of invisible radiation inside and outside our homes. All of this radiation is energy, which is universally measured in Joules (J) and when we consider the rate of expenditure of energy (joules/seconds) we obtain a measure of the number of watts.
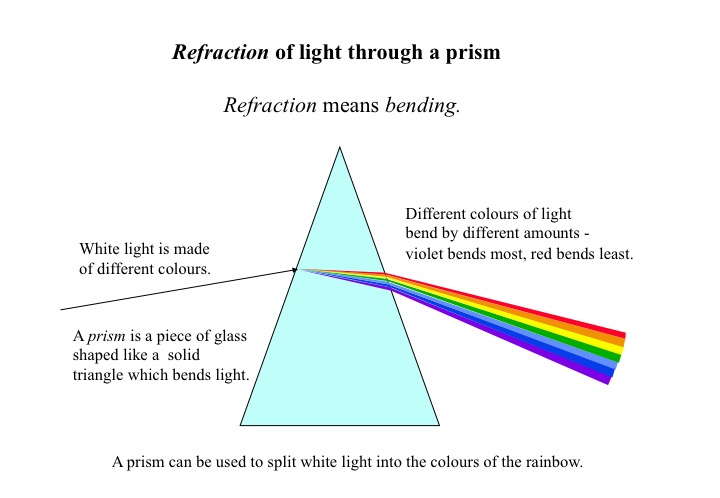
Figure H06.3: A ray of white light that strikes a glass prism from the left, is broken up into its component colours as it exits on the right. The spectrum of visible light ranges from low energy / long wavelength red light to high energy / short wavelength purple light.
Light, by definition, is what we can see, i.e. the visible part of the electromagnetic spectrum, and light itself is composed of all of the colours of the rainbow from red at the low energy/long wavelength end of the spectrum, to purple at the high energy/short wavelength end. Most of the time we think of light as a waveform, with a frequency (v) and a wavelength (l) related to the speed of light (c) by the equation:
c = v . l
However, when we reach extremely low intensities of light, it is sometimes necessary to remember the wave-particle duality of light, that is, light can also be represented by particles called photons. A photon is the smallest "piece" of light that is possible in physics, rather like a water molecule is the smallest "piece" of water in chemistry. It is said that, in principle, a human eye is capable of perceiving a single photon. However, in reality (and assuming our eye is perfect - which may not be the case as we get older) our eye is somewhat de-tuned for practical reasons, and will only respond to about 100 photons per second. It is also the case that the response of human eyes to light varies with wavelength, and that the optimum response occurs at 555 nm (green light).
THE INVERSE SQUARE LAW
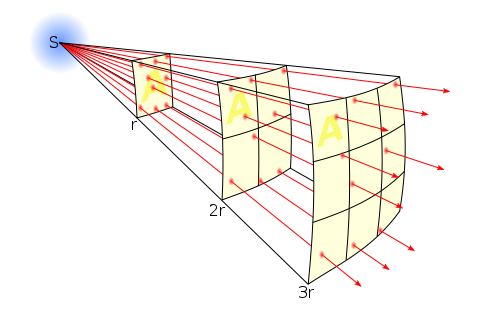
Figure H06.4: The Inverse Square Law
All light is subject to the inverse square law which says that the energy is dissipated (spreads out) according to the square of the distance travelled. Thus energy E = 1/r2. A luminous intensity measured at a distance of 1 metre will reduced by a factor of 4 (0.25) at a distance of 2 metres (E = 1/22) and by a factor of 9 (0.11) at 3 metres. Clearly, It will be reduced by a factor of 100 (0.01) at a distance of 10 metres (E=1/102).
LUMINOUS FLUX
As we have seen above, there is a complication when considering measurements and calculations of light energy, because often we are interested in what can be seen by the human eye, but there are many wavelengths that are not visible to the human eye. So a distinction is made between two different kinds of light energy. A package of light energy containing both visible and invisible energy is called radiant flux; a package containing only visible energy is called luminous flux. For much of my arguments below, I shall consider only luminous flux.
Notice that the light from a candle is generated by converting the chemical energy (i.e. burning) of the fuel (candle wax) into heat and light energy, which is dissipated from the flame equally in all directions.
The unit of luminous flux is the lumen (lm). It is defined as the light energy emitted per second within unit solid angle (measured by the unit, steradian, abbreviated sr) by a uniform point source of 1 unit luminous intensity.
If a light source emits one candela of luminous intensity uniformly across a solid angle of one steradian, the total luminous flux emitted into that angle is one lumen (1 cd·1 sr = 1 lm). Alternatively, a uniform light source of 1 cd emits a total luminous flux of 4π (i.e. 12.6) lumens, because if we think of a sphere with the light source at the centre of the sphere, there are 4π steradians of volume around it.
The lumen can be thought of as a measure of the total visible light in some defined beam or angle, or emitted from some source. But, as we have seen, because of the varying sensitivity of the eye across the range of wavelengths, the number of candelas or lumens from a source strictly depends on the spectral content.
The difference between the units lumen and lux is that the lux takes into account the area over which the luminous flux is spread. A flux of 1000 lumens, concentrated into an area of one square metre, lights up that square metre with an illuminance of 1000 lux. The same 1000 lumens, spread out over ten square metres, produces a dimmer illuminance of only 100 lux. Mathematically, 1 lx = 1 lm/m2.
A source radiating a power of one watt of light in the color for which the eye is most efficient (a wavelength of 555 nm, in the green region of the optical spectrum) has luminous flux of 683 lumens. So a lumen represents at least 1/683 watts of visible light power, depending on the spectral distribution.
THE CONVENTIONAL CANDLE
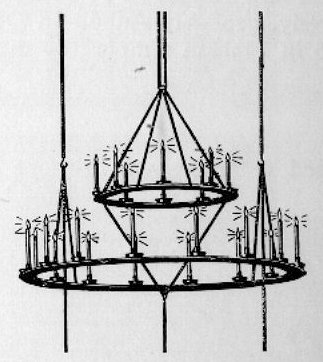
Figure H06.5: The chandelier constructed in the Eddystone lighthouse by John Smeaton was designed for a light of 24 candles.
We shall discover that this subject is necessarily given to a number of approximations for a variety of reasons, so we need to adopt a pragmatic approach to our science. For many years, candles have been approximately 1 foot in length (300 mm) and 1 inch in thickness (25.4 mm). In his Eddystone lighthouse of 1759, the British lighthouse engineer, John Smeaton used a chandelier comprised of 24 candles with approximately these dimensions. He also recorded that 5 candles weighed 2 pounds, so we can calculate that each candle weighed 181 g.
The first pragmatic approximation is to say that, in Figure H06.4, for example, we have a conventional candle, and that its output, or luminous flux, is 1 candela, which falls upon 1 steradian of area at a distance of 1 metre from the flame. If we divide by 4π, and also by 683 (to convert into watts), we arrive at the light energy from a candle falling on 1 square metre of area at a distance of 1 metre as 0.0184 W.
I am now going to branch in two directions. Firstly, let us consider the human eye, which has an area considerably smaller than 1 m2. Taking a typical iris radius in total darkness as 0.005 metres, the total sensory area of a human eye is calculated as 7.85 x 10-5 m2. From this we calculate that the eye receives 9.15 x 10-9 W at 1 metre distant. Now it is said that the eye can detect a minimum threshold of 100 photons per second, which is equivalent to 3.57 x 10-17 W. Using the inverse square law, we calculate that a single candle could in theory be seen at a distance of 16 Km. However, we must recognise thast there are many factors that will reduce this visibility. For example, weather conditions such as bright moonlight or rain in the atmosphere will significantly reduce this visibility. The efficiency of the human eye is no small consideration. And our calculation used a value for iris radius that assumed total darkness. In reality, the iris could be much smaller, and this would reduce the distance much further. For example, an iris radius of 2 mm reduces the maximum visibility to 6.4 Km. So there are a number of uncertainties in our calculations that make it difficult to be precise.
For my second approach, I am going to consider a slightly more realistic situation. Now we know that Smeaton used 24 candles in his lighthouse on the Eddystone. He also wrote in his diary that when he was on board the Neptune Buss (the ship he used to travel the 20 Km distance from Plymouth to the Eddystone), he could see the light from his lighthouse when he was close to the shoreline of Plymouth Hoe, and that the light was equivalent to a star of magnitude 3 or 4, naturally depending upon the weather conditions. (Smeaton was a man of great precision, experienced in astronomy, and we can accept his observations as being quite accurate).
We learned above that 1 candela is the luminous intensity, in a given direction, of a source that emits monochromatic radiation of frequency 540×1012 hertz and that has a radiant intensity in that direction of 1 / 683 watt per steradian, i.e. 0.001464 W sr-1. In the case of a sphere of radius 1 m, 1 sr = 1 m2. So let us say that 24 candles alight in Smeaton's Tower would give 24 x 0.001464 W /m2 at the lantern glass = 0.0351 W/m2. This energy of illumination is reduced by the inverse square law to 8.785 x 10-11 W/m2 at 20 Km - the approximate distance to Plymouth Hoe.
Allowing for the small size of the human eye, this energy must be reduced by the appropriate factor, so we get 6.9 x 10-15 W entering an eye with an iris of 5 mm, i.e. under perfectly dark conditions. In practice, it would not be perfectly dark for an observer, whose iris might have a smaller radius of, perhaps, 2 mm, in which case this amount would be reduced still further to about 1.1 10-15 W.
Now let us check out Smeaton's observations comparing the light from his lighthouse with that from stars. He estimated that the brightness of his lighthouse light was comparable to a star of magnitude 3 or 4.
A brief explanation is required. In astronomy, the apparent magnitudes of stars are measured on a scale where negative numbers are brighter and positive numbers are darker. The scale is not logarithmic to the base 10, but the difference between each unit is x2.5. Therefore, a star of magnitude 4 is 2.5x dimmer than a star of magnitude 3. The Sun, being the brightest thing we see on Earth is large and negative at -26.74. The dimmest star visible to the naked eye is at 6.5. (The use of the word 'apparent' simply means that it is as we see them; it takes no account of how far away stars are. Thus the Sun is by no means the brightest star in absolute terms, it's just that other stars are a lot further away so the Sun appears brighter because it is closest.)
If we take some standard values from astronomy as follows: the apparent luminosity of the Sun at the surface of the Earth = -26.74, the luminous intensity of the Sun at its surface as 3.846 x 1026 W and the distance of the Sun from the Earth as 1.5 x 1011 m. Now we can calculate that the energy received by an eye seeing a star of apparent magnitude 3 is 2.17 x 10-14 W, and for a star of magnitude 4 is 8.63 x 10-15 W. From these calculations, with answers firmly in the range of 10-14 to 10-15, and allowing for inevitable errors of approximation implicit in the approach, we confirm that Smeaton was correct in his observation.
WHAT IS THE THRESHOLD FOR VISIBILITY OF LIGHT BY A HUMAN EYE?
We considered above that a human eye can detect about 100 photons per second. If we use the standard physics values of 3 x 108 m/s for the speed of light (c), and the value for Planck's constant (h) of 6.6 x 10-34 Js, we take the optimum wavelength (l) visible to the eye as 555 x 10-9 m and calculate the energy (E) of one photon by the formula E = (h x c)/l, i.e. E= 3.567 x 10-19 J. So for 100 photons per second, the eye is receiving 3.567 x 10-17 W. Any smaller amount is invisible.
We can use this threshold value to determine how far a light can be visible, given that as the distance from the light to the observer increases, the energy diminishes according to the inverse square law. Let's try it out...
HOW FAR CAN A LIGHT BE SEEN?

Figure H06.6: A single candle used to represent an ancient aid to navigation.
Let's begin by considering a single candle. For the moment we shall ignore the curvature of the Earth and the effect known as the horizon.
Consider 1 candle placed at a distance of 1 metre from a glass window of area 1 m2. For a sphere of radius 1 metre, the equivalent of a steradian is 1 m2, and we know that the luminous energy falling on the window is 0.001464 W/m2. Adjusting now to the area of the human eye, we get a value (E1) of 9.151 x 10-9 W. If this energy decreases over distance until the eye is at such a distance (d) that it can only just see the equivalent of 100 photons per second, i.e. 3.567 x 10-17 W (E2) then we can calculate the distance from the inverse square law thus: d = sqrt (E1/E2), i.e. 22.7 Km.
If we do the same calculation based upon the threshold of visibility of a star being at a magnitude of 6.5, then the minimum amount of energy received by the eye is 9.96 x 10-16 W and this occurs at a distance of 4.53 Km. These calculations would indicate that the minimum level of light visibility is greater than 100 photons per second, but there are many errors and approximations associated with each method and we cannot be too strict in our interpretations. Amongst other possibilities for discrepancy, the calculation is sensitive to the values of energy we use because there is a square of the distance involved.
CONCLUSIONS
The above calculations have shown a number of things:
1. The light from a single candle placed in a window by a monk or a hermit can be seen at a distance of approximately 5 Km in good weather conditions, based upon the limit of observability used in astronomy. This clearly justifies such procedures used in earlier centuries. Lights of greater luminosity would clearly be more effective.
2. Smeaton's use of 24 candles in his lighthouse is calculated to have a maximum visibility of 22.2 Km, based upon the limit of observability used in astronomy. This accords well with his own observation that at a distance of about 19 Km (12 miles), in good weather, the light was equivalent to a star of about magnitude 3 or 4.